上文中，我们主要介绍了优化分析的基本类型。

优化分析在不同领域中有着广泛的应用，本文主要介绍优化方法在结构设计中的应用，即结构优化设计。

与优化方法类似，对于结构优化问题的描述也可分为：

• 目标函数，即结构设计的目标，通常有质量最小、刚度最大和基频最大等；
• 优化空间，即优化变量的取值范围，如结构尺寸、材料参数、局部形状、结构形状和整体拓扑优化形式等；
• 约束条件，包括结构尺寸范围、体积或质量范围、最大/小应力或位移，以及各种关于优化变量的函数等。

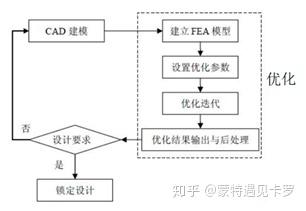
结构优化有很多种形式，通常可分为以下四类：

• 尺寸优化
• 形状优化
• 形貌优化
• 拓扑优化

除了拓扑优化会改变结构的拓扑以外，其余三种优化均不会改变结构的拓扑形式。

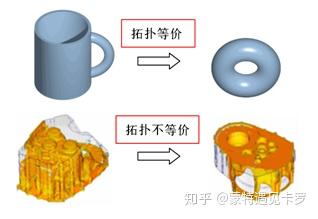
尺寸优化是最基本的结构优化，通常可分为两种：

• 优化梁板等截面参数，如梁的截面尺寸和板的厚度等，这种类型不需要更新几何和网格；
• 优化模型的几何尺寸，如模型的一些整体特征尺寸、局部圆孔半径、方孔的长宽等，这种类型则需要更新几何和网格。

尺寸优化技术相对较成熟，各种优化方法均可应用，大多采用基于撒点的方法和梯度的方法，也可以采用启发式算法。

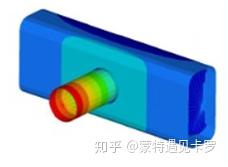
形状优化和形貌优化有一些相似之处，有时被一起讨论。

形状优化分为两类：

• 节点位置的优化，与尺寸优化类似；
• 连续体的开孔形状，如圆孔还是方孔等、倒角，圆倒角还是方倒角、和边界形状等，理论上属于优化方法中的泛函极值问题，其解法较多，有基于变分法的解析算法；有基于优化方法的数值算法；也有基于工程经验的直观准则法等。

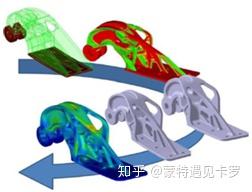
形状优化主要应用于飞机、列车、汽车等流线型设计；同时也是处理应力集中问题的有效方法之一。

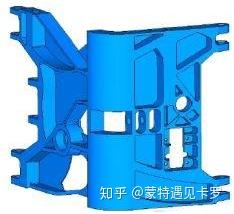
形貌优化和形状优化类似，一般应用于钣金件的结构加强筋设计上，利用冲压形成压痕的加工工艺添加加强筋，可以看作是广义的形状优化中的边界形状设计。通常通过网格扰动优化实现；此外，利用拓扑优化的方法也可以实现类似的加强筋优化设计。

前面几种结构优化方法均不改变结构的拓扑形式。

拓扑优化探讨结构间的连接方式、内部的开孔、位置等信息。由于解的空间过大，因此，拓扑优化相对困难。

拓扑优化可分为以下两类：

• 探讨部件之间的装配或连接拓扑关系：这类问题难度较大，目前应用相对较少，对于这类问题，尤其是桁架系的拓扑结构，可以通过其他方式等价处理实现；
• 探讨零件的结构形式：目前这类问题的拓扑优化是结构优化的一个热门方向；拓扑优化的结构通常无法通过传统的加工工艺实现，而配合当前“3D”打印(增材制造)技术，则可有效解决复杂结构形式的成型加工问题；不过目前增材制造技术并不算成熟，加工的可靠性、一致性、成本以及周期等问题均制约着其大规模应用。

目前主流的拓扑优化过程：

• 将待设计区域划分为若干个有限元单元；
• 依据计算结果，按照一定的规则，减少或增加单元的密度或权重；
• 重复上条，直到迭代完成；
• 形成带孔的连续体，实现拓扑优化。

这种方法本身就是一种演化方法，理论上解释性相对较弱，结果也相对不可捉摸；不过相比其他领域的优化，对于有经验的设计师而言，结构优化结果还是相对容易预测的。

事实上，拓扑优化还存在很多问题，本文仅介绍基本的原理，不做过多的细节讨论。

拓扑优化目前不是很成熟，尽管有多种方法，目前主流的商用软件采用的是“变密度”法；有趣的是，拓扑优化是一个“减材”的过程，而加工是一个“增材”的过程。

在结构设计中，通常会遇到多目标优化问题，如多种指标、多种工况等。目前还没有统一的解决方法，主流的处理方法有以下几种：

• 寻找“帕累托最优”(Pareto Optimal)，也叫做“非劣解”。帕累托最优解简单的解释就是：给定一个向量，在解空间无法找到另外的一个向量，使得所有目标变得最优，这个向量就是帕累托最优解；换言之，就是为了使一些目标变优，必定要“损害”另外的一些目标；这就是“非劣解”名称的由来。通常帕累托最优解有多个，它们形成一个帕累托最优解集；这些最优解集中的解对应的目标目标函数值同样构成目标函数集，这个函数集被称为帕累托最优前沿(Pareto front)；这是多目标优化的一种常见定义，NSGA-Ⅱ是它的一种常用算法；这部分相关内容较多，目前就暂时介绍到这里。

• 保留一个主要目标，将其他目标修改为约束，这也是一种常见的处理方法，一般可以将重要性不那么大的目标和变化范围较小的目标转为约束条件，或者不同目标之间轮换修改为约束，最后再综合取最优解
• 改变目标函数，将多目标重新构造为一个目标函数，不同的目标之间通过加权叠加处理。

在结构优化中，各种优化方法的应用没有明确的界限，选择哪种优化方法需要通过各方面去评估。此外，目前对于多目标结构优化还尚未达到较高程度的共识，优化方法也在不断的完善。

-完-

公众号同步更新：数联科技工作室

公众号内有更多内容！